A Brief History of Statistical Learning
- 1800s Legendre and Gauss: Linear Regression
- 1970s Generalized
linear models (non-linear relationships was computationally infeasible) - 1980s Classification and
regression trees - 2000s Machine Learning
https://zakharus.medium.com/data-science-timeline-305ef75dceb6
1800s Legendre and Gauss: Linear Regression
- describing the relation between two variables with the best fitting curve
1870-1970s Classical Statistics
- formalized statistical test
- t-test e.g., William Sealy Gosset's 1908 paper in Biometrika working for Guinness Brewery
2000s Machine Learning
- complex data points (sentences, images, DNA-sequences)
instead of numeric variables - models with "uncountable" parameters, fitted to the data with computing power
https://www.medrxiv.org/content/10.1101/2020.07.17.20155150v1.full
2010s "Artificial Intelligence"

- deep neural networks (efficient matrix multiplication on GPUs)
- Generative Adversarial Networks that learn to produce
- Reinforcement Learning
https://openai.com/dall-e-2/
Structure of Supervised Learning Problems
- model () describes how one or many predictors ()
relate to a predicted variable :
| Speed | Heart Rate | Linear Regression |
| Expression values of different genes | Diagnosis of a disease | kNN-Classificator |
| Input text | Pixels in a picture | Deep Learning |
 Nomenclature
Nomenclature
- input variables (predictors, independent variables, features)
- e.g, age, years on the job, education
- output variable (response or predicted/dependent variable)
- e.g., income
we use large letters, when we speak about the random variable, [Hasties]
| id | : Income | : Years of Education | : Seniority | : Age |
|---|---|---|---|---|
| 1 | 45000 | 10 | 7 | 34 |
| 2 | 50000 | 20 | 5 | 63 |
| ... | ... | ... | ... |
- We assume that there is some relationship between and and different predictors, .
- is a fixed but unknown function of ,
- is a random error term, which is independent of and has mean zero.
- represents the systematic information that provides about
Applications
- Why estimate ?
- we build models to
- predict the future
what should we offer out next employee? - understand the world (interpretation)
should it do a master?
- predict the future
Prediction
- We want to make a prediction about
- the future - stock prices
- an unknown property - does the patient have cancer?
-
- a hat symbol ( ) indicates a prediction
- is often a black box, in machine learning the model is a prediction based on the data
- We probably make an prediction error
- We are interested in the accuracy of
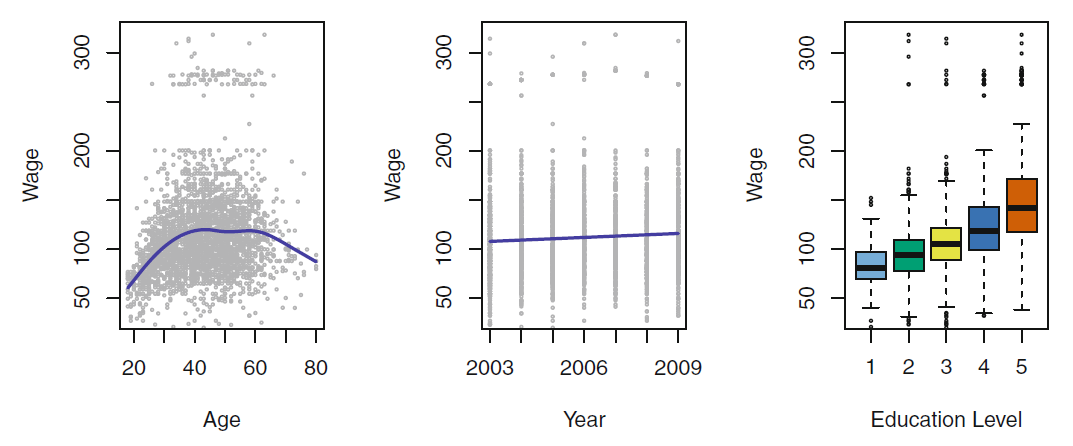
Prediction Example
- Can we predict the income based on the
education and years of seniority in the job
| id | : Income | : Years of Education | : Seniority |
|---|---|---|---|
| 1 | 45000 | 10 | 7 |
| 2 | 50000 | 20 | 5 |
| ... | ... | ... |
- the model is the blue area
- we can plug in eduction () and seniority ()
- to get an prediction on the income ()
- we do not care what looks like as long we make small errors for each observation (red dot)
[Hasties]
Interpretation
- how is affected as change?
- must not be a black box, because we need to know its exact form
- We are interested in the parameters of the model
- How strong is the relationship between the response and each predictor?
- How much more will a person earn for each year of education?
- Which predictors are associated with the response?
- Does seniority have any impact at all?
- Can the relationship between and each predictor be adequately summarized
using a linear equation, or is the relationship more complicated?- Will the income increase in a stable way?
- Is there a safe level of alcohol consumption?
 Interpretation or prediction?
Interpretation or prediction?
: prediction
: interpretation
- What's the gas price next summer?
- Do students in the front row get better grades?
- Given an x-ray picture, does the patient have lung cancer?
- What has the lager influence on weight: sugar or fat intake?
 How do we estimate ?
How do we estimate ?
- training data ( observations of our sample, rows in a table) to train, or teach, our method how to estimate
(e.g., income based in education and seniority) -
- the value of the th of predictors
- for observation of observations
- where and .
-
- We use the small to indicate the vector of all predictors of observation (i.e., a row)
-
- We use the capital to indicate the vector of the values of the th predictor (i.e., a column)
- response variable for the th observation.
- Then our training data consist of
- Our goal is to apply a statistical learning method to the training data
in order to estimate the unknown function . - so that for any observation .
- There are parametric and non-parametric methods (compare blue planes in the prediction example)
2.2.2 Parametric and non-parametric Models
 Learning objectives
Learning objectives
You will be able to
- differentiate parametric and non-parametric models
- calculate accuracy measures of regression models
- interpret in (training-set) and out-of-sample (test-set) accuracy in terms of model flexibility, bias, variance, and over-fitting
 Parametric Methods
Parametric Methods
-
Step 1: assumption about the functional form or shape of .
- e.g., a simple linear form
- e.g., a simple linear form
-
Step 2: training data to fit the model.
- we need to estimate the parameters .
- find values of these parameters such that
Variable
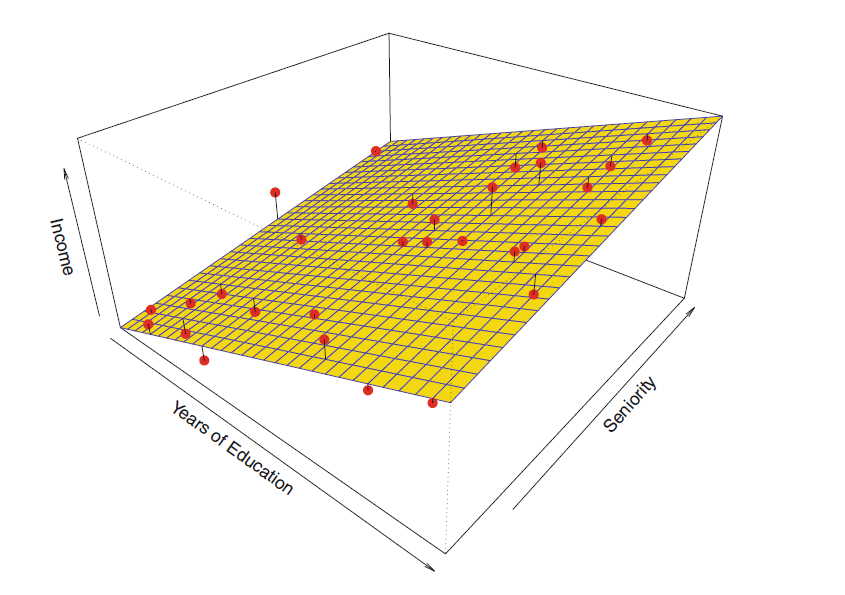
Parametric model of income explained by years of education and years on the job (seniority)
Matrix Representation for Linear Models
- … value of predictor of observation
- … are all so is the bias term
(i.e., the intercept of the linear regression model)
- Observation 1
- Observation 2
Parametric Methods
- form is fixed, but we can tweak three parameters to improve the fit ()
- is the intercept
-
: uneducated workers without eduction get a salary of
-
: one year of education results in higher salary
-
: one year of working experience results in higher salary
-
linear regression is a parametric and relatively inflexible approach
- it can only generate linear functions
- only two factors (lines) to interpret
 Task
Task
Non-parametric Methods
- no explicit assumption about the functional form of
- but some kind of algorithm of
- close to the data points
- without being too rough or wiggly
- e.g., a hand-drawn line is a non-parametric model
 Over-fitting
Over-fitting
- more common with flexible, non-parametric methods
- perfect prediction for any point in the training data
- probably not a good prediction for points that are not in the training data
 Sample split in Training and Test Set
Sample split in Training and Test Set
- Training data: the data we use for building the mode (e.g., finding /fitting the right parameters for the model)
- Test data: Hold-out sample, that we can use to test how well the model performs on unseen data
- more important with prediction tasks
Trade-Off Between Prediction Accuracy and Model Interpretability
- parametric models are usually easier to interpret
Which to use for prediction and interpretation?
- Non-parametric model tend to be more powerful
and therefore better for predictions - Parametric models are less flexible but have
clear parameters ( sometimes called ) that are
easier to understand for interpretation
 Task
Task
Assessing Model Accuracy
- There is no free lunch in statistics:
no one method dominates all others over all
possible data sets.
- How to decide for any given set of data which method produces the best results?
https://xkcd.com/2048/
 Measuring the Quality of Fit
Measuring the Quality of Fit
- the error of each prediction tells us how well the predictions match the observed data
- Mean squared error () is a common accuracy measure,
 Training vs Test Set
Training vs Test Set
- Many methods minimize the during training (training , in-sample )
- in general, we do not really care how well the method works during training on the training data,
- but how our methods works on previously unseen test data (out-of-sample )
Fitting Data with a low flexibility Model
-
- (i.e., the mean of all red dots of the training data)
- only one parameter
-
black: prediction
-
red: Training data (medium fit)
-
blue: Test data (good fit)
Fitting Data with a medium flexibility Model
-
- two parameters and
-
black: prediction
-
red: Training data (good fit)
-
blue: Test data (good fit)
Fitting Data with a high flexibility Model
-
- three parameters , ,
- black: prediction
- red: Training data (very good fit)
- blue: Test data (poor fit)
 Task
Task
The Bias-Variance Trade-Off and Over-Fitting
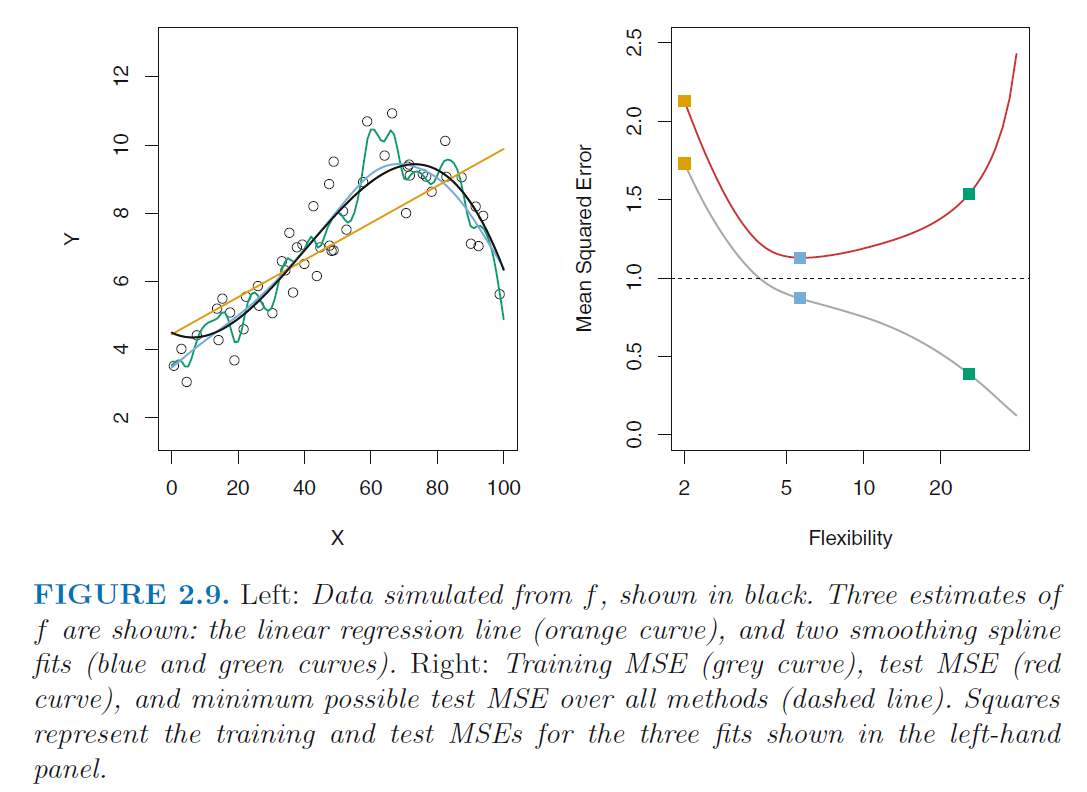
- The higher the flexibility
- the lower the on the training data
- the higher the on the test data
- U-shape in the test MSE is the result of two competing properties of statistical learning methods
- Variance refers to the amount by which would change
if we estimated it using a different training data set. - Bias refers to the error that is introduced by approximating
a real-life problem, which may be extremely complicated,
by a much simpler model.
See Hasties p. 34 correct formula
- Black line: Error on the test set
- more flexible (complex, often non-parametric) models have higher variance but lower bias
- they can fit the data better (low bias), but are more influenced by the data (high variance)